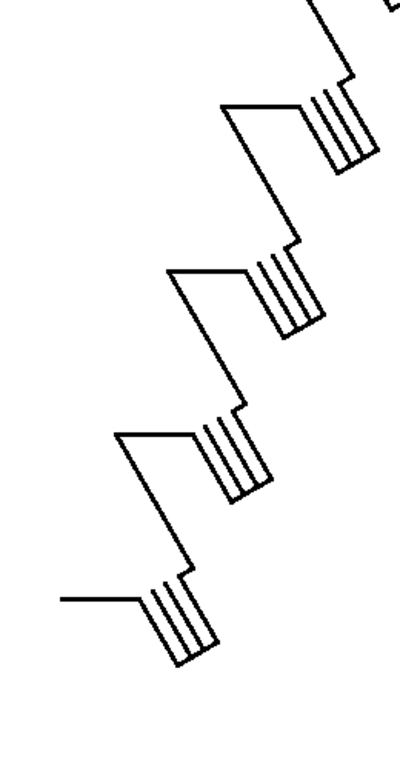
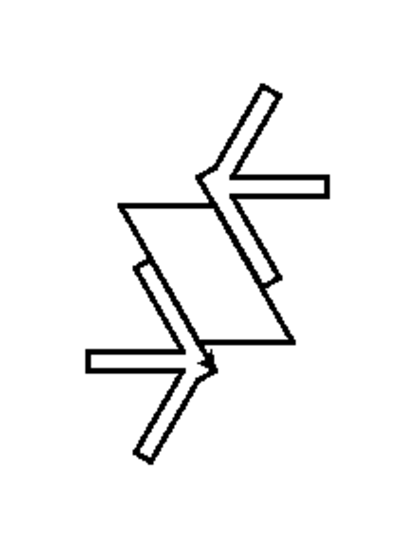
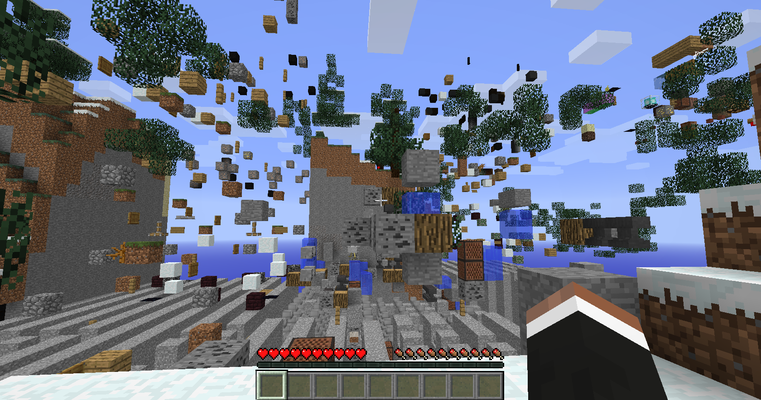
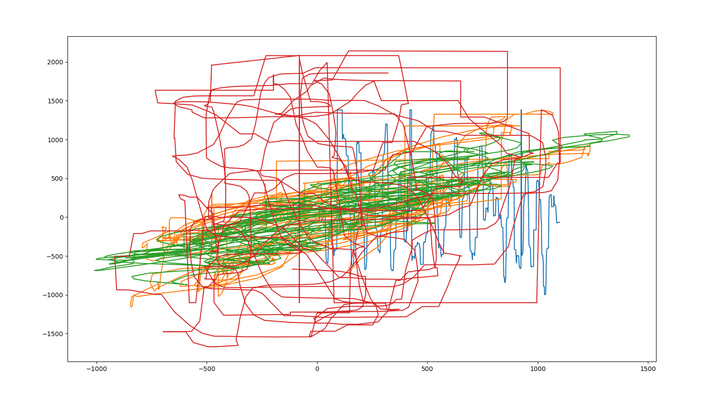
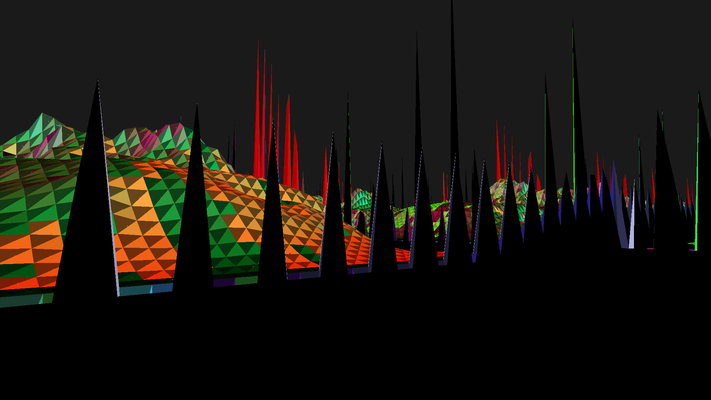
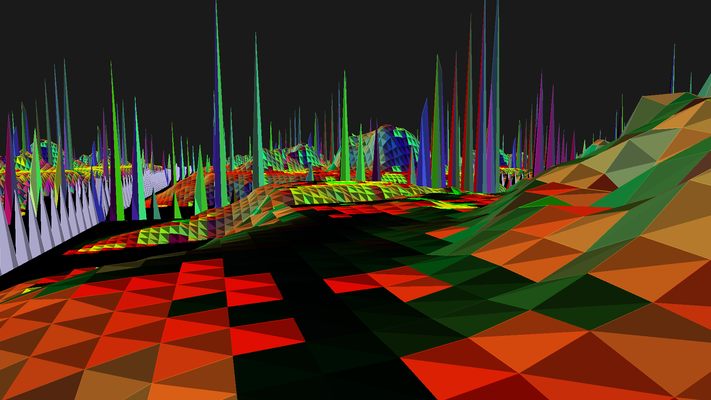
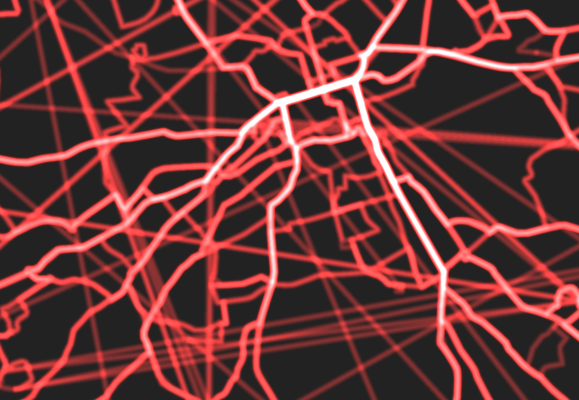
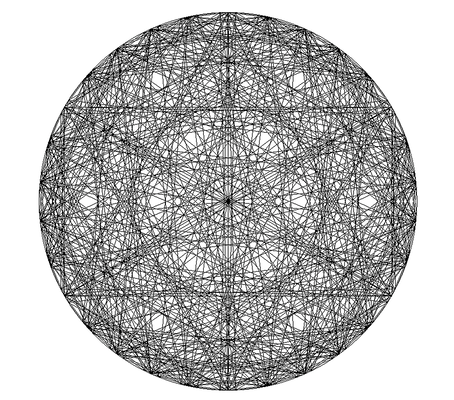
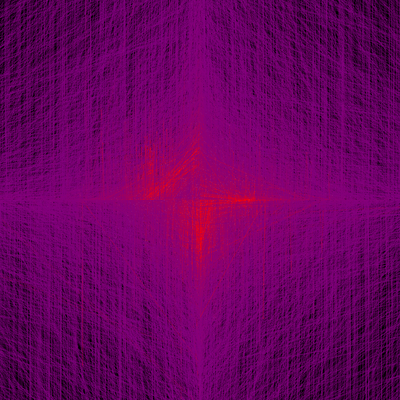
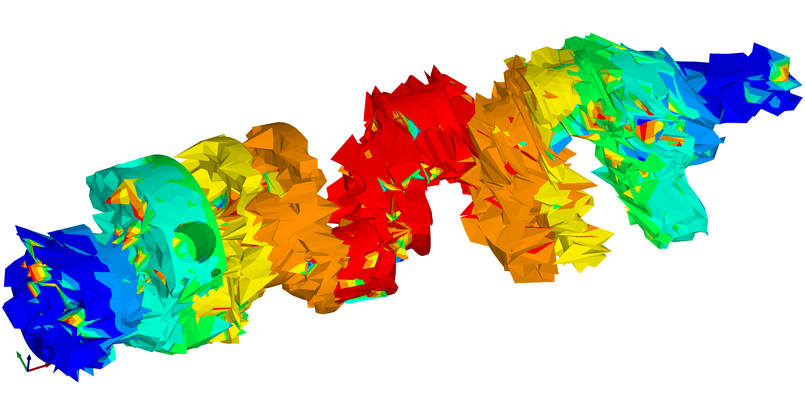
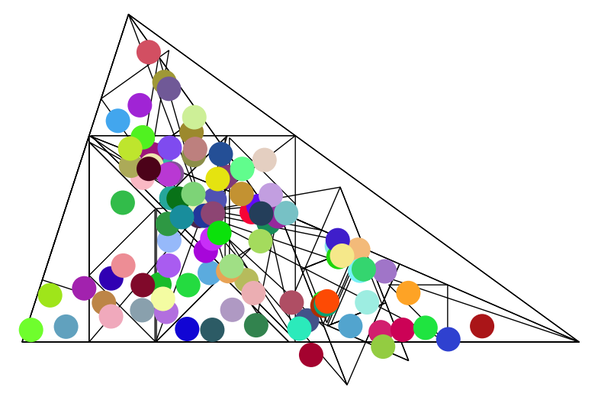
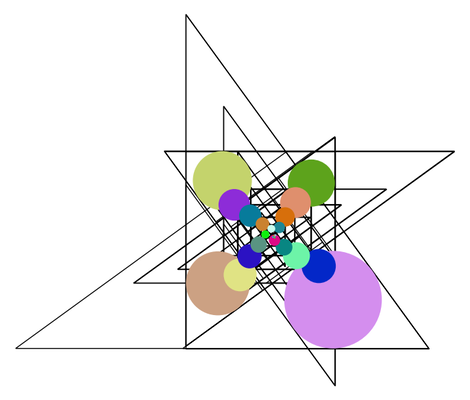
Welcome to the Glitch Gallery, an online exhibition of pretty software bugs! This is a museum of accidental art, an enthusiastic embrace of mistakes, a celebration of emergent beauty. Learn more?
Below you can browse the exhibits in our collection. If you have ever encountered such an accidental artwork yourself, we invite you to submit it to us!